基础知识

矩阵乘法概述

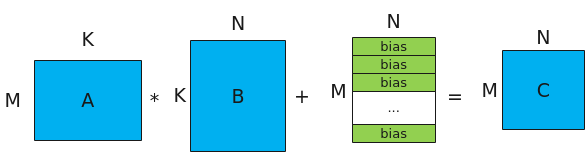
MatMul的计算公式为：C = A * B + bias，其示意图如下。

• A、B为源操作数，A为左矩阵，形状为[M, K]；B为右矩阵，形状为[K, N]。
• C为目的操作数，存放矩阵乘结果的矩阵，形状为[M, N]。
• bias为矩阵乘偏置，形状为[1,N]。对A*B结果矩阵的每一行都采用该bias进行偏置。

矩阵乘法数据流

在了解矩阵乘法数据流之前，需要先回顾一下几个重要的存储逻辑位置的概念：

• 搬入数据的存放位置：A1，用于存放整块A矩阵，可类比CPU多级缓存中的二级缓存；
• 搬入数据的存放位置：B1，用于存放整块B矩阵，可类比CPU多级缓存中的二级缓存；
• 搬入数据的存放位置：A2，用于存放切分后的小块A矩阵，可类比CPU多级缓存中的一级缓存；
• 搬入数据的存放位置：B2，用于存放切分后的小块B矩阵，可类比CPU多级缓存中的一级缓存；
• 结果数据的存放位置：CO1，用于存放小块结果C矩阵，可理解为Cube Out；
• 结果数据的存放位置：CO2，用于存放整块结果C矩阵，可理解为Cube Out；
• 搬入数据的存放位置：VECCALC，一般在计算需要临时变量时使用此位置。

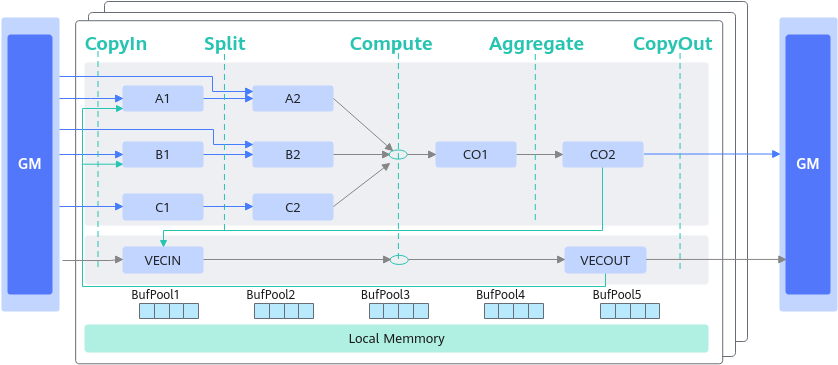
矩阵乘法数据流指矩阵乘的输入输出在各存储位置间的流向。逻辑位置的数据流向如下图所示：

• A矩阵从输入位置到A2的数据流如下（输入位置可以是GM或者VECOUT）：GM->A2，GM->A1->A2；VECOUT->A1->A2。
• B矩阵从输入位置到B2的数据流如下（输入位置可以是GM或者VECOUT）：GM->B2，GM->B1->B2；VECOUT->B1->B2。
• 完成A2*B2=CO1计算。
• CO1数据汇聚到CO2：CO1->CO2。
• 从CO2到输出位置（输出位置可以是GM或者VECIN）：CO2->GM/CO2->VECIN。

数据格式

在完成Matmul矩阵乘法时，涉及到两种分形格式ND和NZ。

• ND：普通格式，N维张量。
• NZ：为满足AICore中Cube计算单元高性能计算的需要，引入该特殊格式。

  ND –> NZ的变换过程为：

  (..., N，H, W )->pad->(..., N, H1*H0, W1*W0)->reshape->(..., N, H1, H0, W1, W0)->transpose->(..., N, W1, H1, H0, W0)

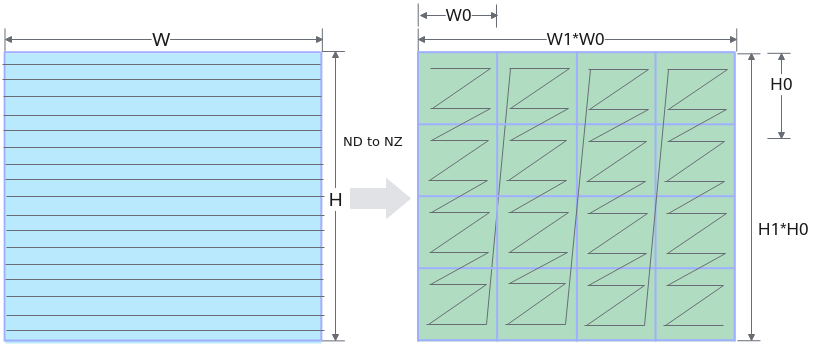
  如下图所示 （W，H）大小的矩阵被分为（H1*W1）个分形，按照column major排布，形状如N字形；每个分形内部有（H0*W0）个元素，按照row major排布，形状如z字形。所以这种数据格式称为NZ（大N小Z）格式。

  

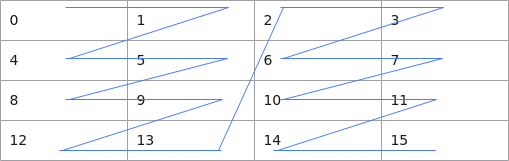
  下面我们再通过一个具体的例子来深入理解ND和NZ格式的数据排布区别。假设分形格式为2*2，如下图所示4*4的矩阵，ND和NZ格式存储两种情况下，数据在内存中的排布格式分别为：

  ND: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

  NZ: 0, 1, 4, 5, 8, 9, 12, 13, 2, 3, 6, 7, 10, 11, 14, 15

  

数据分块（Tiling）

• 多核切分

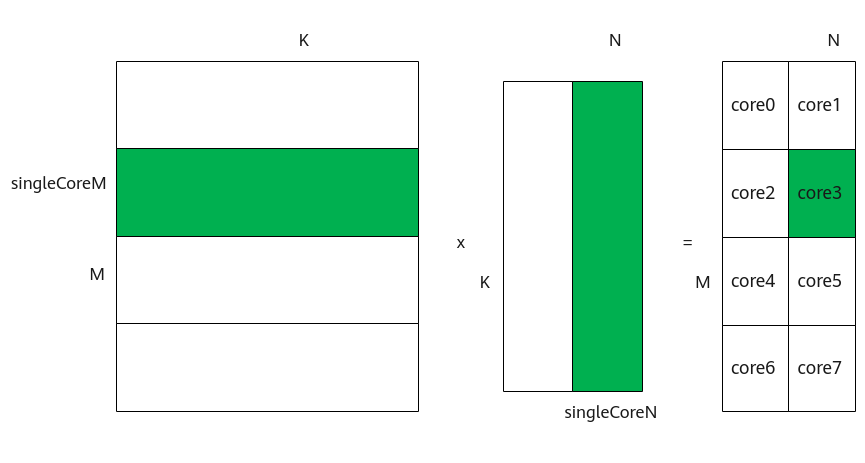
  为了实现多核并行，需要将矩阵数据进行切分，分配到不同的核上进行处理。切分策略如下图所示：

  • 对于A矩阵，沿着M轴进行切分，切分成多份的singleCoreM，单核上处理SingleCoreM * K大小的数据。
  • 对于B矩阵，沿着N轴进行切分，切分成多份的singleCoreN，单核上处理K * SingleCoreN大小的数据。
  • 对于C矩阵，SingleCoreM * K大小的A矩阵和K * SingleCoreN大小的B矩阵相乘得到SingleCoreM * SingleCoreN大小的C矩阵，即为单核上输出的C矩阵大小。

  比如，下图中共有8个核参与计算，将A矩阵沿着M轴划分为4块，将B矩阵沿着N轴切分为两块，单核上仅处理某一分块（比如图中绿色部分为core3上参与计算的数据）：SingleCoreM * K大小的A矩阵分块和SingleCoreN* K大小的B矩阵分块相乘得到SingleCoreM * SingleCoreN大小的C矩阵分块。

  

• 核内切分

  大多数情况下，Local Memory的存储，无法完整的容纳算子的输入与输出，需要每次搬运一部分输入进行计算然后搬出，再搬运下一部分输入进行计算，直到得到完整的最终结果，也就是需要做核内的输入切分。切分的策略如下所示：

  • 对于A矩阵，沿M轴进行切分，切分成多份的baseM；沿K轴进行切分，切分成多份的baseK。
  • 对于B矩阵，沿N轴进行切分，切分成多份的baseN，沿K轴进行切分，切分成多份的baseK。
  • 对于C矩阵，A矩阵中baseM * baseK大小的分块和B矩阵中 baseK * base N大小的分块相乘并累加，得到C矩阵中对应位置baseM * base N大小的分块。比如，图中结果矩阵中的蓝色矩阵块5是通过如下的累加过程得到的：a*a+b*b+c*c+d*d+e*e+f*f。

  

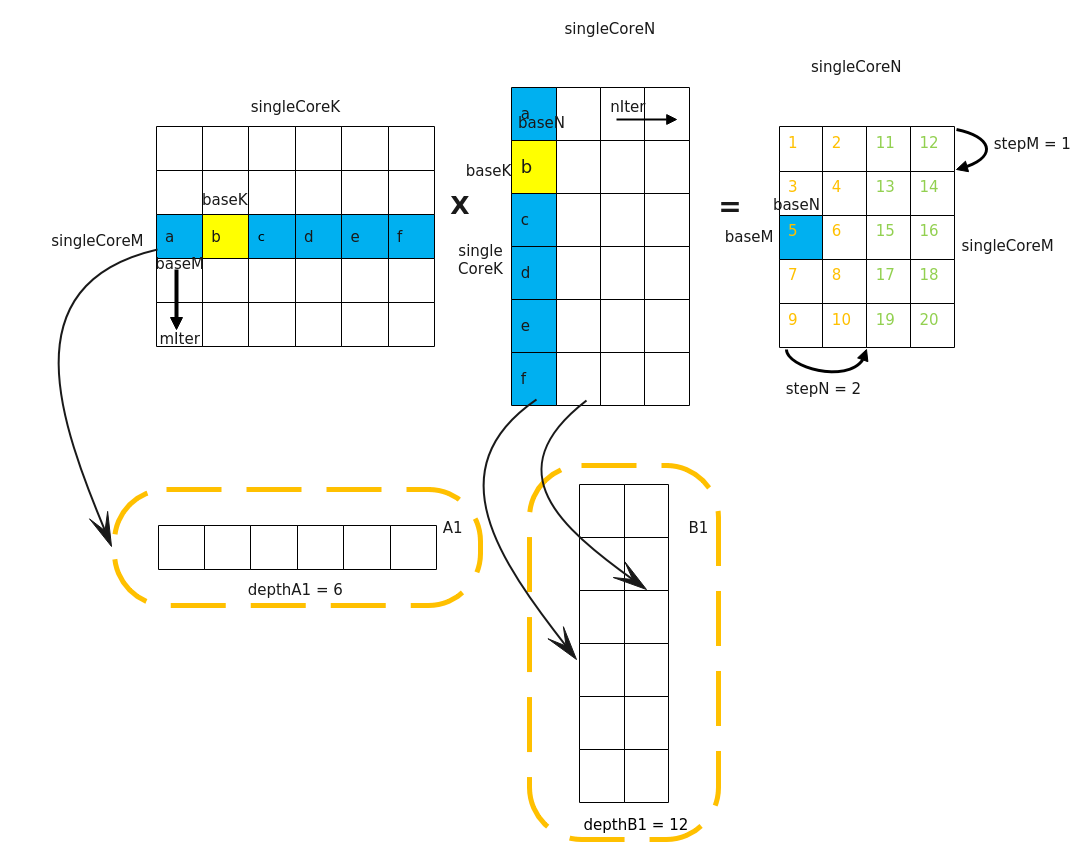
  除了baseM, baseN, baseK外，还有一些常用的tiling参数，其含义如下：

  • iterateOrder：一次Iterate迭代计算出[baseM, baseN]大小的C矩阵分片。Iterate完成后，Matmul会自动偏移下一次Iterate输出的C矩阵位置，iterOrder表示自动偏移的顺序。
    • 0代表先往M轴方向偏移再往N轴方向偏移
    • 1代表先往N轴方向偏移再往M轴方向偏移
  • depthA1，depthB1：A1、B1上存储的矩阵片全载A2/B2的份数，A2、B2存储大小分别是baseM * baseK，baseN * baseK。
  • stepM，stepN：stepM为左矩阵在A1中缓存的bufferM方向上baseM的倍数。stepN为右矩阵在B1中缓存的bufferN方向上baseN的倍数。