大模型参数规模大,存储并优化这些参数需要的内存大大超出设备的上限,超大的训练数据和参数规模也使得训练时间非常长。所以模型参数必须要能分割到多个AI处理器设备上,利用大量设备分布式地完成大模型的训练。分布式训练必然带来通信开销,另外这些通信算子也会引起计算精度问题,进而影响模型收敛。
本节将介绍Megatron-LM的模型分割和计算并行算法,以及这些算法可能引起的计算精度问题。
- 流水线并行将模型的不同层放置到不同的设备上。这种方式可以在不同设备上并行执行不同的模型阶段,从而提高效率。
- 张量并行将模型的层内部进行分割,将某一层的计算分配到不同的设备上,再通过集合通信拿到完整的计算结果。
需要注意的是,流水线并行是伪并行,需要结合数据微批次(micro-batch)使用才能减少NPU或GPU的空闲等待时间(空泡),而张量并行是真并行,不会引起空泡,但两者都会带来很大的通信开销。
词嵌入输入层embedding张量并行
embedding层的作用是为给定一个长度为s的输入token id序列,输出这个序列对应s个h维向量。token所在的词汇表长度一般记为v,v大约在3万到5万。h一般是一万以上。所以词嵌入层的参数量为v*h,大约在亿量级。因为embedding层的运算是查表,它的切割比较直接明了,只需要将词汇表分成连续的段,每段的词向量存放在一个AI处理器上即可。例如token id为0~3999的词向量存在NPU0上,4000~7999的词向量存在NPU1上。给定token id输入序列,分别在NPU0、NPU1上查找词向量,找不到的词向量置为0。查找完毕后每个NPU设备做一次TP组的allreduce即可在每个NPU设备上获得完整的s*h维词embedding矩阵。如下图所示:
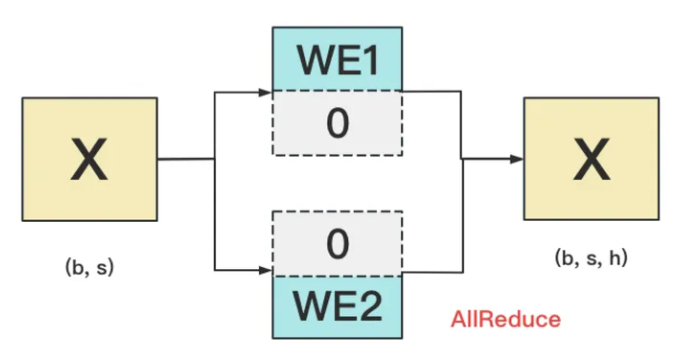
并行词嵌入层的前向allReduce累加本质上是拼接,所以不会引起浮点精度问题。X是输入id序列,反向过程也不需要计算X的梯度。
线性层张量并行
Transformer中会将输入向量通过线性层转成QKV矩阵。线性层是一个h*h权重矩阵,如果h是一万,那么此权重矩阵规模也是亿级。线性层权重矩阵有两种切分方式,行切分和列切分。
列切分后输入矩阵X分别在NPU0和NPU1上与切分后的子矩阵W1、W2相乘,得到Y1、Y2,将Y1、Y2简单合并就得到最终结果Y。列切分后的反向传播过程这里略过。列切分后的前向计算过程如下:
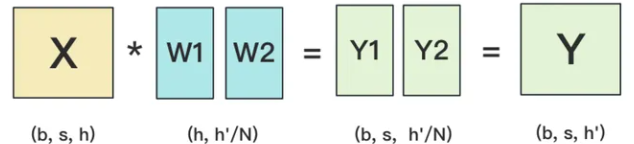
列切分的前向只涉及结果的简单合并,所以不会引起精度问题。但是反向过程X的梯度,涉及W1、W2两个(实际情况下张量并行度一般是8)传播路径,需要做allreduce通信算子计算,需要考虑精度问题。例如OLMo-7B就使用FP32进行梯度reduce,而Falcon-7B使用BF16进行梯度reduce。一般来说,参数越多,TP并行度越高,使用BF16做梯度reduce的难度越大。
如果权重矩阵按行切分成W1、W2,则输入X需要按列切分成X1、X2到各NPU设备,否则维度不一致无法做矩阵乘法。各个设备矩阵乘法的结果Y1=X1*W1和Y2=X2*W2需要做allreduce同步将Y1、Y2加起来才能得到X*W的最终结果,正向过程有累加运算,需要考虑是否会引起精度误差。如下图所示:

MLP层切分
MLP层有一个线性层A将输入向量维度扩大四倍(或其他倍数),再经过一个激活层GELU,最后通过一个线性层B再降维到输入的维度。通过如下公式表示:
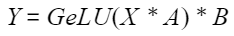
其中X尺寸为s*h,A尺寸为h*4h,B尺寸为4h*h。最优切分方案是对A采用列切分,对B采用行切分,这样可以简化计算过程并降低集合通信量。MLP的切分正向过程有allreduce矩阵累加,反向过程需要将X的梯度做allreduce,需要考虑累加带来的浮点精度问题。
流水线并行
流水线并行在水平方向上将模型的transformer层放在不同的NPU上,一份训练数据的完整计算在多个NPU上完成。因为后一层的输入需要依赖前一层的输出,如果仅有一个batch数据,那么NPU大部分时间都在等待,不能达到加速计算的目的。为了解决NPU设备的空等(计算空泡)问题,一个大的batch会被切分成多个小的微batch,通过精心设计的流水线调度算法减小计算空泡时间,例如1F1B虚拟流水线并行算法。流水线并行在一个数据批次结束时需要在NPU之间同步累积各层的梯度信息(flush),需要考虑累加带来的浮点精度问题。