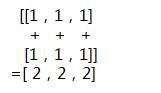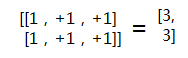算子基本概念

算子名称（Name）

算子的名称，用于标志网络中的某个算子，同一网络中算子的名称需要保持唯一。如下图所示Conv1，Pool1，Conv2都是此网络中的算子名称，其中Conv1与Conv2算子的类型为Convolution，表示分别做一次卷积运算。

图2 网络拓扑示例

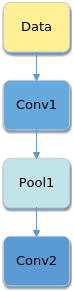
算子类型（Type）

网络中每一个算子根据算子类型进行算子实现的匹配，相同类型的算子的实现逻辑相同。在一个网络中同一类型的算子可能存在多个，例如上图中的Conv1算子与Conv2算子的类型都为Convolution。

张量（Tensor）

Tensor是算子计算数据的容器，TensorDesc（Tensor描述符）是对Tensor中数据的描述，TensorDesc数据结构包含如下属性如表1所示。

形状（Shape）

张量的形状，以(D0, D1, … ,Dn-1)的形式表示，D0到Dn是任意的正整数。

如形状(3,4)表示第一维有3个元素，第二维有4个元素，(3,4)表示一个3行4列的矩阵数组。

在形状的小括号中有多少个数字，就代表这个张量是多少维的张量。形状的第一个元素要看张量最外层的中括号中有几个元素，形状的第二个元素要看张量中从左边开始数第二个中括号中有几个元素，依此类推。例如：

物理含义我们应该怎么理解呢？假设我们有这样一个shape=(4, 20, 20, 3)。

假设有一些照片，每个像素点都由红/绿/蓝3色组成，即shape里面3的含义，照片的宽和高都是20，也就是20*20=400个像素，总共有4张的照片，这就是shape=(4, 20, 20, 3)的物理含义。

图3 示意图：

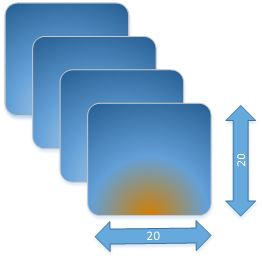
如果体现在编程上，可以简单把shape理解为操作Tensor的各层循环，比如我们要对shape=(4, 20, 20, 3)的A tensor进行操作，循环语句如下：

produce A {
  for (i, 0, 4) {
    for (j, 0, 20) {
      for (p, 0, 20) {
        for (q, 0, 3) {
          A[((((((i*20) + j)*20) + p)*3) + q)] = a_tensor[((((((i*20) + j)*20) + p)*3) + q)]
        }
      }
    }
  }
}

轴（axis）

轴是相对Shape来说的，轴代表张量的shape的下标，比如张量a是一个5行6列的二维数组，即shape是(5,6)，则axis=0表示是张量中的第一维，即行。axis=1表示是张量中的第二维，即列。

例如张量数据[[[1,2],[3,4]], [[5,6],[7,8]]]，Shape为(2,2,2)，则轴0代表第一个维度的数据即[[1,2],[3,4]]与[[5,6],[7,8]]这两个矩阵，轴1代表第二个维度的数据即[1,2]、[3,4]、[5,6]、[7,8]这四个数组，轴2代表第三个维度的数据即1，2，3，4，5，6，7，8这八个数。

轴axis可以为负数，此时表示是倒数第axis个维度。

N维Tensor的轴有：0 , 1, 2,……，N-1。

图4 轴示意图：

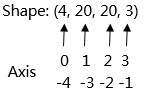
权重（weight）

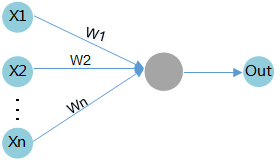
当输入数据进入计算单元时，会乘以一个权重。例如，如果一个算子有两个输入，则每个输入会分配一个关联权重，一般将认为较重要数据赋予较高的权重，不重要的数据赋予较小的权重，为零的权重则表示特定的特征是无需关注的。

如图5所示，假设输入数据为X1，与其相关联的权重为W1，那么在通过计算单元后，数据变为了X1*W1。

图5 权重计算示例

偏差（bias）

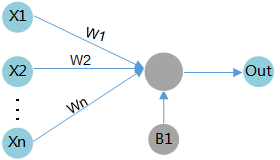
偏差是除了权重之外，另一个被应用于输入数据的线性分量。它被加到权重与输入数据相乘的结果中，用于改变权重与输入相乘所得结果的范围。

如图6所示，假设输入数据为X1，与其相关联的权重为W1，偏差为B1，那么在通过计算单元后，数据变为了X1*W1+B1。

图6 偏差计算示例

广播

TBE支持的广播规则：可以将一个数组的每一个维度扩展为一个固定的shape，需要被扩展的数组的每个维度的大小或者与目标shape相等，或者为1，广播会在元素个数为1的维度上进行。

例如：原数组a的维度为（2, 1, 64），目标shape为（2, 128, 64），则通过广播可以将a的维度扩展为目标shape（2, 128, 64）。

TBE的计算接口加、减、乘、除等不支持自动广播，要求输入的两个Tensor的shape相同，所以操作前，我们需要先计算出目标shape，然后将每个输入Tensor广播到目标shape再进行计算。

例如，Tensor A的shape为（4, 3, 1, 5），Tensor B的shape为（1, 1, 2, 1），执行Tensor A + Tensor B ，具体计算过程如下：

1. 计算出目标shape C。
   图7 示例1
   

   取Tensor A与Tensor B中每个维度的大值，作为目标Shape，C（4, 3, 2, 5）。

2. 调用广播接口分别将Tensor A与Tensor B扩展到目标Shape C。

   

   需要广播的tensor的shape需要满足规则：每个维度的大小或者与目标shape相等，或者为1。

   若不满足以上规则，则无法进行广播，如下所示：

   

3. 调用计算接口，进行Tensor A + Tensor B。

降维-Reduction

降维有很多种算子，例如TensorFlow中的Sum、Min、Max、All、Mean等，Caffe中的Reduction算子，此处以Caffe中的Reduction算子为例进行讲解，Reduction是将多维数组的指定轴及之后的数据做降维操作。