更多场景

动态shape场景

在算子实现章节，已经介绍了简单的固定shape矢量算子的kernel侧实现，算子的shape、数据类型都是固定的；在实际的算子开发场景中，这些信息是支持动态变化的，场景会更加灵活和复杂。下文重点进行动态shape与固定shape差异点的介绍。

最主要的区别是：动态Shape场景下，输入的Shape是未知的。一些与输入Shape相关的变量（比如每次搬运的块大小等），需要通过Tiling计算出来，然后传递到kernel侧，kernel侧使用该参数进行后续的计算。

算子实现章节中固定shape的算子样例中，TILE_NUM（每个核上总计算数据分块个数）、BLOCK_LENGTH（每个核上总计算数据大小）、TILE_LENGTH（每个分块大小）等是固定的数值。

constexpr int32_t TOTAL_LENGTH = 8 * 2048;                            // total length of data
constexpr int32_t USE_CORE_NUM = 8;                                   // num of core used
constexpr int32_t BLOCK_LENGTH = TOTAL_LENGTH / USE_CORE_NUM;         // length computed of each core
constexpr int32_t TILE_NUM = 8;                                       // split data into 8 tiles for each core
constexpr int32_t BUFFER_NUM = 2;                                     // tensor num for each queue
constexpr int32_t TILE_LENGTH = BLOCK_LENGTH / TILE_NUM / BUFFER_NUM; // each tile length is separated to 2 part, due to double buffer

如果需要将上述代码转换为动态shape，需要在核函数定义中增加Tiling参数，在host侧计算Tiling参数并传入，然后基于Tiling参数计算得到singleCoreSize（每个核上总计算数据大小）、tileNum（每个核上总计算数据分块个数）、tileLength（每个分块大小）等变量。

__aicore__ inline void Init(GM_ADDR x, GM_ADDR y, GM_ADDR z, uint32_t totalLength, uint32_t tileNum)
{
    ASSERT(GetBlockNum() != 0 && "block dim can not be zero!");
    this->blockLength = totalLength / GetBlockNum();
    this->tileNum = tileNum;
    ASSERT(tileNum != 0 && "tile num can not be zero!");
    this->tileLength = this->blockLength / tileNum / BUFFER_NUM;
    // ...

}

extern "C" __global__ __aicore__ void add_custom(GM_ADDR x, GM_ADDR y, GM_ADDR z, GM_ADDR workspace, AddCustomTilingData tiling)
{
    KernelAdd op;
    op.Init(x, y, z, tiling.totalLength, tiling.tileNum);
    op.Process();
}

shape非对齐场景

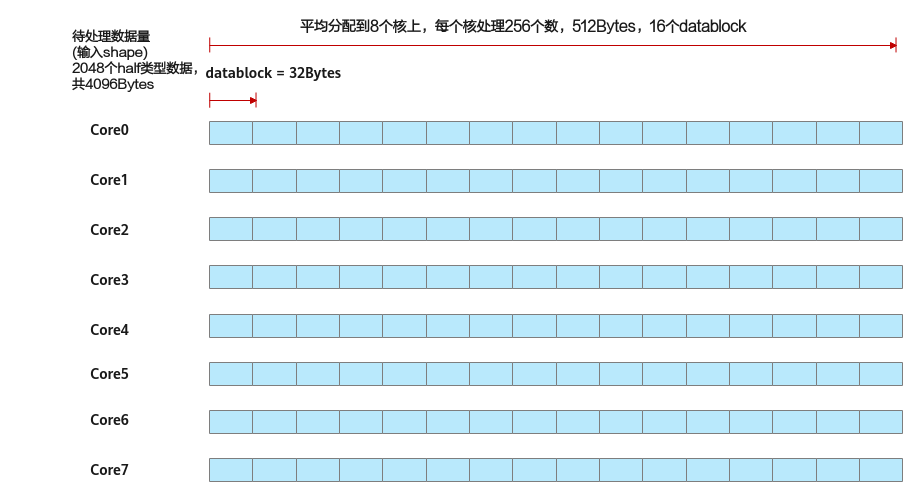
上文描述的都是shape对齐的场景：如下图中的示例，算子的输入shape为（1，2048），支持的数据类型为half类型，可以对齐到一个datablock的大小（32B），也可以平均分配到每个核上（假设使用8个核），每个核上处理256个数，16个datablock。

图1 shape对齐场景

针对一些非对齐shape，比如算子的输入shape为（1，1999），支持的数据类型为half类型，既无法对齐到一个datablock的大小（32B），也无法平均分配到每个核上，需要一些特殊的Tiling处理方法。

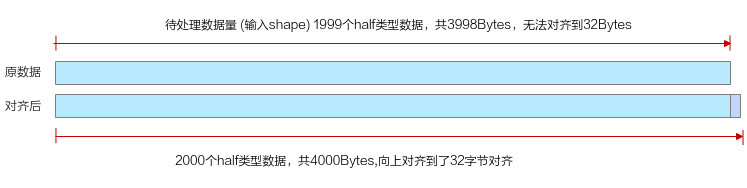
因为昇腾AI处理器在进行数据搬运和Vector计算时，对于搬运的数据长度和UB首地址都有必须32B对齐的要求，首先待处理数据需要先保证对齐到datablock的大小。该场景下后续搬运和计算的处理细节请参考非对齐处理。下图和代码片段展示了将数据对齐到datablock大小的示例：
图2 对齐到datablock大小
```
constexpr uint32_t SIZE_OF_HALF = 2;
constexpr uint32_t BLOCK_SIZE = 32;
constexpr uint32_t ALIGN_NUM = BLOCK_SIZE / SIZE_OF_HALF;
// shape需要对齐到的datablock,假设原totalLength为1999，向上满足32字节对齐后为2000
uint32_t totalLengthAligned = ((totalLength + ALIGN_NUM - 1) / ALIGN_NUM) * ALIGN_NUM;
```

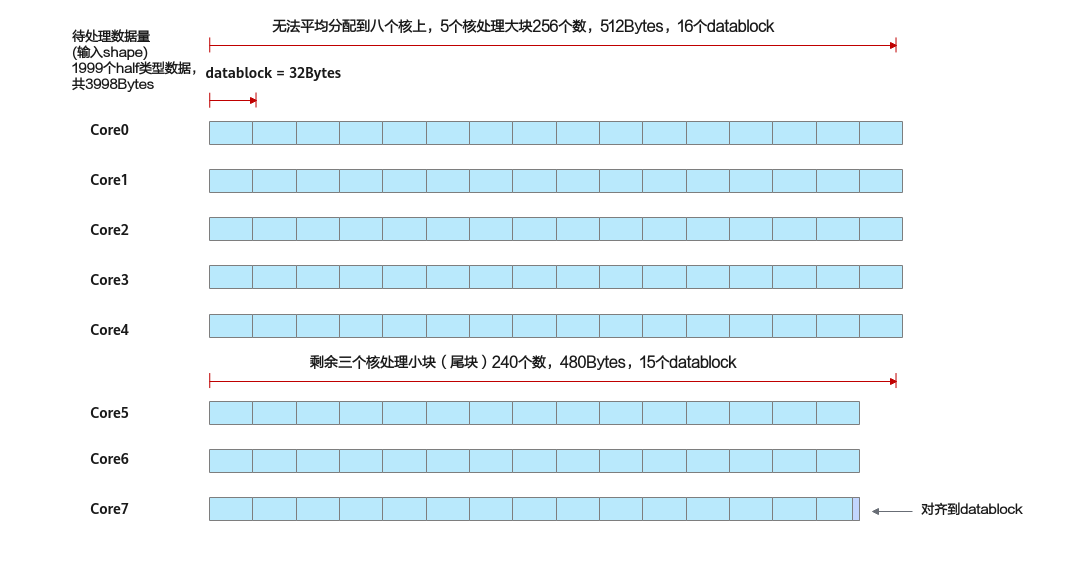
满足datablock对齐后的数据，应尽可能的均分到每个核上。如果无法均分，那么先将可以均分的部分平均分配，剩余的部分分配给部分核，会有部分核多算一个datablock。下图展示了无法均分时将数据进行多核切分的示例。对齐到datablock后为2000个half类型的数据，共125个datablock。125%8结果为15，余数为5，说明：可以均分的部分平均分配，每个核分配到15个datablock；还剩余5个datablock，分配给5个核，所以会有5个核分配到16个datablock，剩余3个核分配到15个datablock。

图3 无法均分到每个核上的示例

基于上文的描述，可以设计如下的Tiling参数：

formerNum：分配到大块的核数
tailNum：分配到小块的核数
formerLength：大块计算的数据量
tailLength：小块计算的数据量
alignNum：一个datablock包含的元素个数

这些Tiling参数的计算方法如下：

constexpr uint32_t BLOCK_DIM = 8;
constexpr uint32_t SIZE_OF_HALF = 2;
constexpr uint32_t BLOCK_SIZE = 32;
// shape需要对齐到的最小单位
constexpr uint32_t ALIGN_NUM = BLOCK_SIZE / SIZE_OF_HALF;
...
uint8_t *GenerateTiling()
{
    // shape需要对齐到的datablock,假设原totalLength为1999，向上满足32字节对齐后为2000
    uint32_t totalLengthAligned = ((totalLength + ALIGN_NUM - 1) / ALIGN_NUM) * ALIGN_NUM;
    // 把所有的数据尽可能均匀地分配到每个核上
    // 如果不能均分,先将可以均分的部分平均分配，剩余的部分分配给部分核，会有部分核多算一个datablock 
    // 通过模的计算，可以得到多算一个datablock的核的数量，也可以得到剩余核的数量
    // eg：1999 对齐后的总数据量为2000个数，核心数为8，一个datablock包含16个数，那么：
    // datablock的总数：2000 / 16 = 125
    // 有5个核会分到16个datablock：125 % 8 =5，可以称之为大块
    // 有3个核会分到15个datablock：8 - 5 = 3，可以称之为小块
    uint32_t formerNum = (totalLengthAligned / ALIGN_NUM) % BLOCK_DIM;
    uint32_t tailNum = BLOCK_DIM - formerNum;
    // 大块计算的数据量：totalLengthAligned / BLOCK_DIM为每个核上计算的元素个数，formerLength为上述元素个数向上32字节对齐的结果
    uint32_t formerLength = ((totalLengthAligned / BLOCK_DIM + ALIGN_NUM - 1) / ALIGN_NUM) * ALIGN_NUM;
    // 小块计算的数据量：totalLengthAligned / BLOCK_DIM为每个核上计算的元素个数，tailLength 为上述元素个数向下32字节对齐的结果
    uint32_t tailLength = (totalLengthAligned / BLOCK_DIM / ALIGN_NUM) * ALIGN_NUM;

...
}

相对应的，在Kernel侧，使用获取到的信息计算得到每个核上的偏移量、每个分块大小的样例如下。

__aicore__ inline void Init(GM_ADDR x, GM_ADDR y, GM_ADDR z, uint32_t formerNum, uint32_t tailNum, uint32_t formerLength, uint32_t tailLength, uint32_t alignNum)
{
    if (GetBlockIdx() < formerNum) {
        this->tileLength = formerLength;
        xGm.SetGlobalBuffer((__gm__ half *)x + formerLength * GetBlockIdx(), formerLength);
        yGm.SetGlobalBuffer((__gm__ half *)y + formerLength * GetBlockIdx(), formerLength);
        zGm.SetGlobalBuffer((__gm__ half *)z + formerLength * GetBlockIdx(), formerLength);
    } else {
        this->tileLength = tailLength;
        xGm.SetGlobalBuffer((__gm__ half *)x + formerLength * formerNum + tailLength * (GetBlockIdx() - formerNum), tailLength);
        yGm.SetGlobalBuffer((__gm__ half *)y + formerLength * formerNum + tailLength * (GetBlockIdx() - formerNum), tailLength);
        zGm.SetGlobalBuffer((__gm__ half *)z + formerLength * formerNum + tailLength * (GetBlockIdx() - formerNum), tailLength);
    }
    pipe.InitBuffer(inQueueX, BUFFER_NUM, this->tileLength * sizeof(half));
    pipe.InitBuffer(inQueueY, BUFFER_NUM, this->tileLength * sizeof(half));
    pipe.InitBuffer(outQueueZ, BUFFER_NUM, this->tileLength * sizeof(half));
}

父主题： 矢量编程