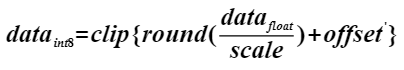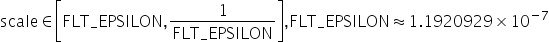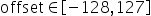量化算法原理
量化常用的算法有二值化、线性量化、对数量化，线性量化又可根据是否有offset细分为对称(Symmetric)，非对称(Asymmetric)两种。AMCT与昇腾芯片配套的是采用线性量化方式，并将对称和非对称量化方式进行了归一，其应用表达式为：
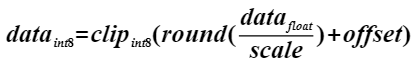
对于量化层数据和权重分别需要提供量化因子scale（浮点数的缩放因子），offset（偏移量）两项，支持的取值范围为：
下面介绍上述表达式的由来。
对称量化算法原理
原始高精度数据和量化后int8数据的转换为：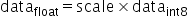
，其中scale是float32的浮点数，为了能够表示正负数，
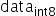采用signed int8的数据类型，通过原始高精度数据转换到int8数据的操作如下，其中round为取整函数，量化算法需要确定的数值即为常数scale：
对权值和数据的量化可以归结为寻找scale的过程，由于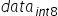
为有符号数，要保证正负数值表示范围的对称性，因此对所有数据首先进行取绝对值的操作，使待量化数据的范围变换为
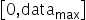，再来确定scale。由于int8在正数范围内能表示的数值范围为[0,127]，因此scale可以通过如下方式计算得到：
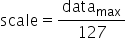
确定了scale之后，int8数据对应的表示范围为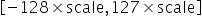
，量化操作即为对量化数据以
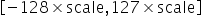进行饱和，即超过范围的数据饱和到边界值，然后进行公式所示量化操作即可。
非对称量化算法原理
与对称量化算法主要区别在于数据转换的方式不同，如下，同样需要确定scale与offset这两个常数。
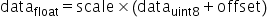
确定后通过原始高精度数据计算得到UINT8数据的转换，既为如下公式所示：
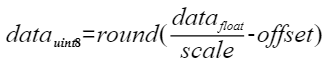
其中，scale是FP32浮点数，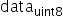
为unsigned int8定点数，offset是int8定点数，其表示的数据范围为
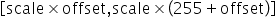。若待量化数据的取值范围为
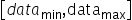，则scale和offset的计算方式如下：
，
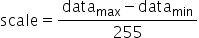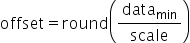
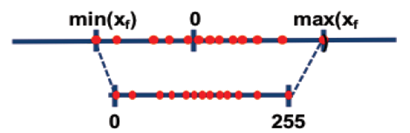
量化数据格式归一
AMCT采用的是归一的量化数据格式，即量化数据格式归一：
通过将非对称量化公式通过简单的数据变换，可以使得量化后的数据与对称量化算法在数据格式上保持一致，均为int格式。具体变换过程如下：
以int8量化为例进行说明，公式符号与之前保持一致，输入原始高精度浮点数据为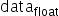
，原始量化后的定点数为
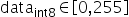，量化scale，原始量化
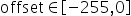（算法要求强制过零点，否则可能会出现精度问题），原始量化的计算原理公式如下：
其中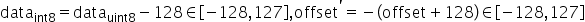
。通过上述变换，可以将量化数据也转成int8格式。确定scale和变换后的offset'后，通过原始高精度浮点数据计算得到int8数据的转换，既为如下公式所示：
