ArithProgression
功能说明
给定起始值,等差值和长度,返回一个等差数列。
实现原理
以float类型,ND格式,firstValue和diffValue输入Scalar为例,描述ArithProgression高阶API内部算法框图,如下图所示。
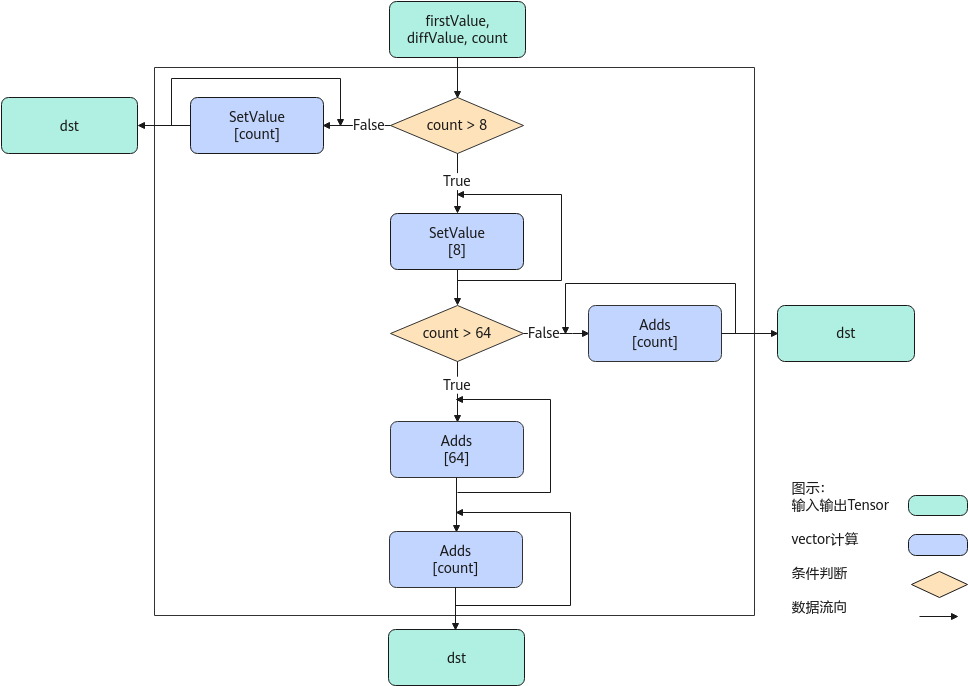
计算过程分为如下几步,均在Vector上进行:
- 等差数列长度8以内步骤:按照firstValue和diffValue的值,使用SetValue实现等差数列扩充,扩充长度最大为8,如果等差数列长度小于8,算法结束;
- 等差数列长度8至64的步骤:对第一步中的等差数列结果使用Adds进行扩充,最大循环7次扩充至64,如果等差数列长度小于64,算法结束;
- 等差数列长度64以上的步骤:对第二步中的等差数列结果使用Adds进行扩充,不断循环直至达到等差数列长度为止。
函数原型
1 2 | template <typename T> __aicore__ inline void ArithProgression(const LocalTensor<T> &dstLocal, const T firstValue, const T diffValue, const int32_t count) |
参数说明
参数名 |
描述 |
|---|---|
T |
操作数的数据类型。 |
参数名 |
输入/输出 |
描述 |
|---|---|---|
dstLocal |
输出 |
目的操作数。dstTensor的大小应大于等于count * sizeof(T)。 类型为LocalTensor,支持的TPosition为VECIN/VECCALC/VECOUT。 |
firstValue |
输入 |
等差数列的首个元素值。 |
diffValue |
输入 |
等差数列元素之间的差值,应大于等于0。 |
count |
输入 |
等差数列的长度。count>0。 |
返回值
无
支持的型号
约束说明
当前仅支持ND格式的输入,不支持其他格式。
调用示例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | #include "kernel_operator.h" template <typename T> class KernelArithProgression { public: __aicore__ inline KernelArithProgression() {} __aicore__ inline void Init(GM_ADDR dstGm, int64_t firstValue, int64_t diffValue, uint32_t count) { firstValue_ = firstValue; diffValue_ = diffValue; count_ = count; dst_global.SetGlobalBuffer(reinterpret_cast<__gm__ T *>(dstGm), count_); pipe.InitBuffer(outDst, 1, (sizeof(T) * count_ + 32 - 1) / 32 * 32); } __aicore__ inline void Process() { CopyIn(); Compute(); CopyOut(); } private: __aicore__ inline void CopyIn() { ; } __aicore__ inline void Compute() { AscendC::LocalTensor<T> dstLocal = outDst.AllocTensor<T>(); AscendC::ArithProgression<T>(dstLocal, static_cast<T>(firstValue_), static_cast<T>(diffValue_), count_); outDst.EnQue<T>(dstLocal); } __aicore__ inline void CopyOut() { AscendC::LocalTensor<T> dstLocal = outDst.DeQue<T>(); const int32_t BLOCK_NUM = 32 / sizeof(T); AscendC::DataCopy(dst_global, dstLocal, (count_ + BLOCK_NUM - 1) / BLOCK_NUM * BLOCK_NUM); outDst.FreeTensor(dstLocal); } private: AscendC::TPipe pipe; AscendC::TQue<AscendC::QuePosition::VECOUT, 1> outDst; AscendC::GlobalTensor<T> dst_global; int64_t firstValue_; int64_t diffValue_; uint32_t count_; }; extern "C" __global__ __aicore__ void kernel_arith_progression_operator(GM_ADDR dstLocal) { KernelArithProgression<half> op; op.Init(dstLocal, 1, 2, 15); op.Process(); } |