指令精度优化

我们可以通过变换公式来避免直接调用精度较低的接口，本小节以vexp为例，以besseli0e算子为例来说明如何通过替换公式的方法提升算子的精度。besseli0e函数是一个偶函数，其图像如下所示。

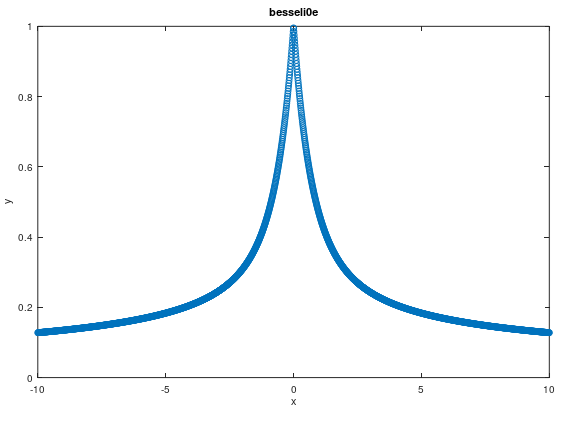
因此我们只需要考虑(0, +∞)区间，通过分段函数，在(0, 3.75)和(3.75, +∞)区间分别使用两个公式拟合，这里我们主要通过(0, 3.75)区间的公式来说明。

假设系数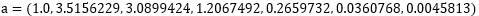

对于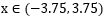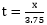，，besseli0e算子公式如下：

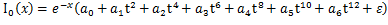
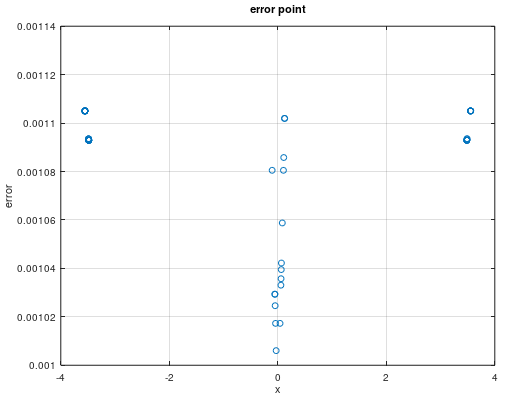
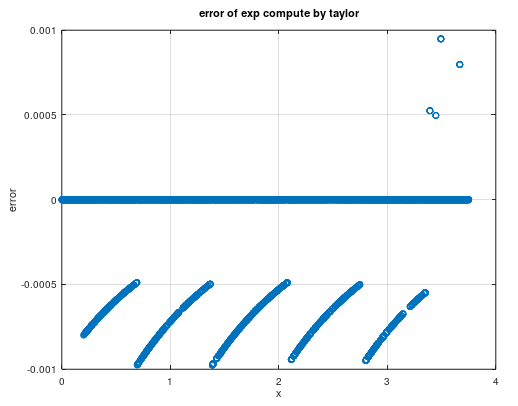
经过测试发现有部分点精度未达到千分之一（我们以精度为千分之一为例进行讲解），我们利用octave可视化分析测试数据，可视化可以帮助我们直观的发现和定位问题。下面我们先把测试数据中所有精度未达标的x画图，如下图所示：

很显然，精度超过0.001的点集中在0附近和3.5附近，结合测试数据确认精度未达标区间是(0, 0.2)和(3.35, 3.75)。我们通过画出定义域上所有点的相对误差进一步分析，发现相对误差的波动接近0.001的区间是(0.7, 1)和(2.7, 3)，和实际精度未达标区间不一致，可见不是公式本身引起的精度问题。

于是我们单独分析精度未达标的区间(0, 0.2)和(3.35, 3.75)，发现大部分x的实际计算结果偏小，且相对误差超过0.001的异常点分布在整个区间，如下图所示

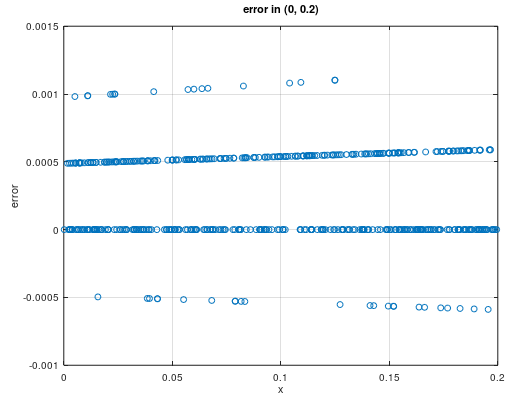
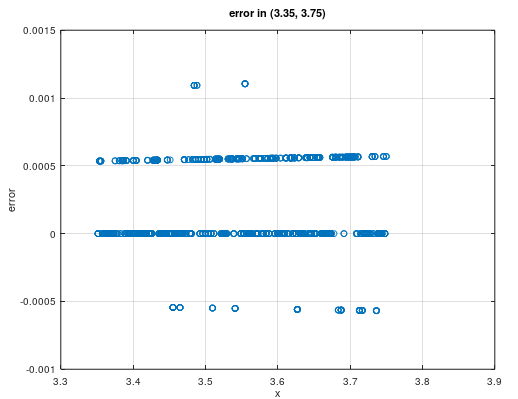
通过可视化分析，我们得出了几个初步结论：

1. 精度未达标区间是(0, 0.2)和(3.35, 3.75)。
2. besseli0e的实际计算值普遍偏小，异常值都是偏小。
3. 精度未达标的点是异常点，和besseli0e的拟合公式本身无关。

结合相对误差的图像和初步结论，分析是vexp指令引起的精度问题，但是我们仍然需要通过分析计算过程的中间结果来确认有问题的计算步骤，具体的，我们在算子中返回中间结果，修改numpy生成的比对数据，利用ST测试来验证每一步的正确性，直到发现精度不达标的计算步骤。由于中间计算过程的误差会随着计算累积或者衰减，这里我们通常会结合实际情况来提高对中间计算过程的要求。以besseli0e为例，我们关注的是使得计算结果偏小的点且相对误差大于万分之八的情况，下图是通过vexp指令计算得到e^x并除以e^x之前和之后的输出值的相对误差分布。

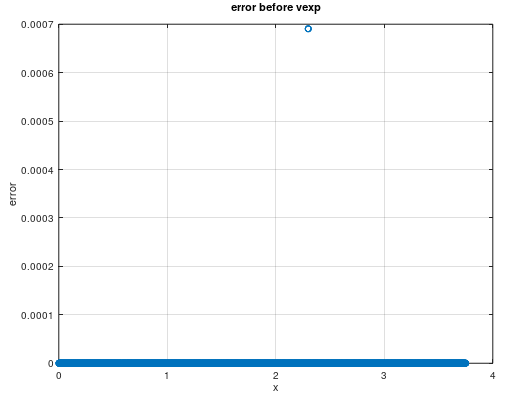
现在，我们可以确定相对误差是由vexp指令引入的，由于vexp指令计算结果偏大，导致besseli0e的计算结果偏小，并使得(0, 0.2)和(3.35, 3.75)区间内的部分点精度达不到千分之一。

由单个指令vexp引起的精度问题，我们就可以考虑通过泰勒展开拟合e^x。通常在x = 0处的泰勒展开（也称麦克劳林展开）公式比较简单，我们目前的精度较低的区间是(0, 0.2)和(3.35, 3.75)，因此首先进行麦克劳林展开，测试展开后的精度，如下图所示：

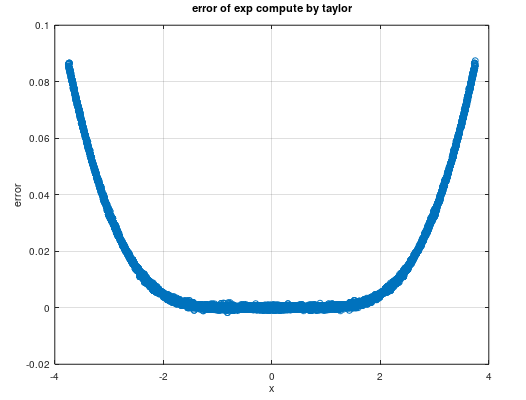
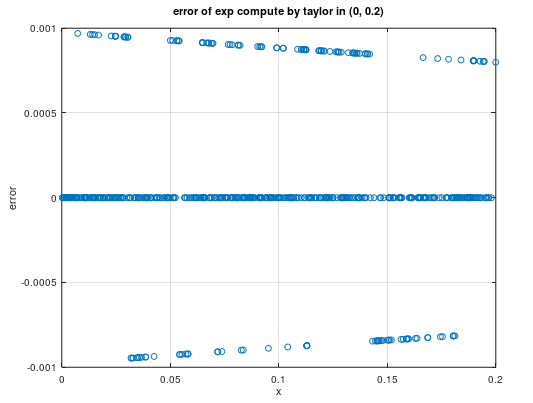
显然(-2, 2)区间外的精度不达标，(3.35, 3.75)区间不能直接使用麦克劳林展开，进一步对我们关心的(0, 0.2)区间进行分析，精度达到了千分之一的要求，最后，我们把泰勒展开实现的e^x加入besseli0e算子进行验证，相对误差如下图所示：

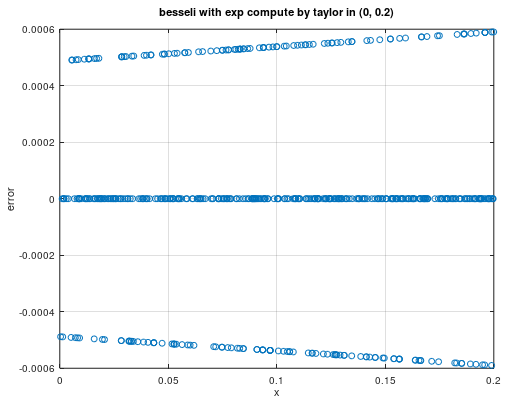
(0, 0.2)精度达标了，由于我们在(-0.2, 0)区间是取绝对值后计算，因此我们可以把(3.35, 3.75)区间的输入映射到(-0.2, 0.2)内计算，根据e^x函数的性质，选择合适的公式进行推导，这里我们用到的是：

x=Qln2 + v, v∈(-0.2, 0.2)

简单计算我们得到Q = 5.1216，将x映射到v，计算得到e^v，再通过e^x=2^Qe^v得到计算结果。到此，我们已经得到了(0, 3.75)的e^x计算公式

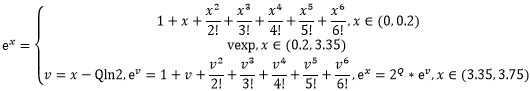
分三个区间选择对应的公式实现e^x，通过ST测试验证，通过泰勒展开实现的e^x满足精度要求，加入besseli0e中验证确认算子精度已达标。

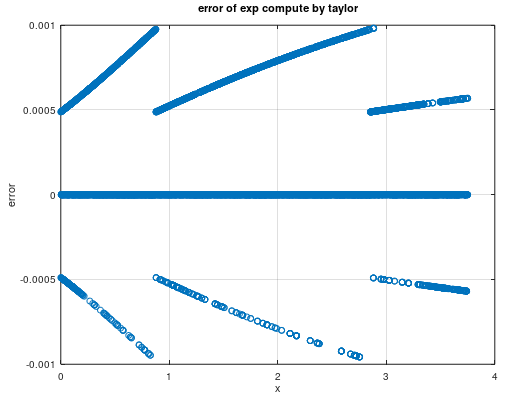
因为公式展开会增加编译、运行时间，降低性能，所以在精度已经满足要求的区间，不建议进行公式展开。在未达标区间进行展开，泰勒展开只能满足展开点附近的小区间内精度达标，因此要先确定展开后公式的精度达标区间，然后推导公式，将不达标的区间的计算映射到达标区间内计算，例如方法1：区间映射。