极限性能分析

文档中的Ascendxxxyy需替换为实际使用的处理器类型。
以matmul算子为例,该用例表示准备处理[160, 240]和[240, 80]的矩阵乘,切割为25个[32, 48], [48, 16]的小矩阵做矩阵乘。通过调用msKPP提供的接口实现的main.py脚本样例如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
from mskpp import mmad, Tensor, Chip def my_mmad(gm_x, gm_y, gm_z): # 矩阵乘的基本数据通路: # 左矩阵A:GM-L1-L0A # 右矩阵B:GM-L1-L0B # 结果矩阵C: L0C(初始化)-GM l1_x = Tensor("L1") l1_y = Tensor("L1") l1_x.load(gm_x) l1_y.load(gm_y) x = Tensor("L0A") y = Tensor("L0B") x.load(l1_x) y.load(l1_y) z = Tensor("L0C", "FP32", [32, 16], format="NC1HWC0") out = mmad(x, y, z, True)() # 对于输出需要返回传出 z = out[0] return z if __name__ == '__main__': with Chip("Ascendxxxyy") as chip: chip.enable_trace() # 使能算子模拟流水图的功能,生成trace.json文件 chip.enable_metrics() # 使能单指令及分PIPE的流水信息,生成Instruction_statistic.csv和Pipe_statistic.csv文件 # 这里进入了对数据切分逻辑的处理,对一大块GM的数据,如何经过拆分成小数据分批次搬入,如何对 # 内存进行分片多buffer搬运,都是属于tiling策略的范畴,这里模拟了单buffer情况, # 将[160, 240]和[240, 80]的矩阵乘,切割为25个[32, 48], [48, 16]的小矩阵分批次进行运算的一个tiling策略 for _ in range(125): in_x = Tensor("GM", "FP16", [32, 48], format="ND") in_y = Tensor("GM", "FP16", [48, 16], format="ND") in_z = Tensor("GM", "FP32", [32, 16], format="NC1HWC0") out_z = my_mmad(in_x, in_y, in_z) in_z.load(out_z) |
使用Python执行以上main.py脚本后,会在当前目录下生成文件指令流水图(trace.json)和指令占比饼图(instruction_cycle_consumption.html),可查看msKPP建模结果。

若当前目录下有相同名称的.csv文件,msKPP工具将无法生成交付件。
指令流水图
流水图文件trace.json,通过查看该文件可以发现在理想的流水中,性能瓶颈的PIPE-MTE2是需要能够一直进行运转的。


在Chrome浏览器中输入“chrome://tracing”地址,将.json文件拖到空白处并打开,通过键盘上的快捷键(W:放大,S:缩小,A:左移,D:右移)进行查看。
图1 trace.json


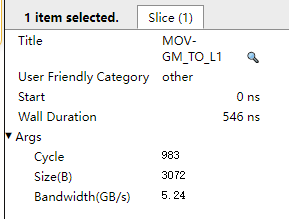
单击流水图中的“MOV-GM_TO_L1”单指令,可查看该指令在当前搬运量及计算量下的cycle数和带宽,如图2所示。
指令占比饼图
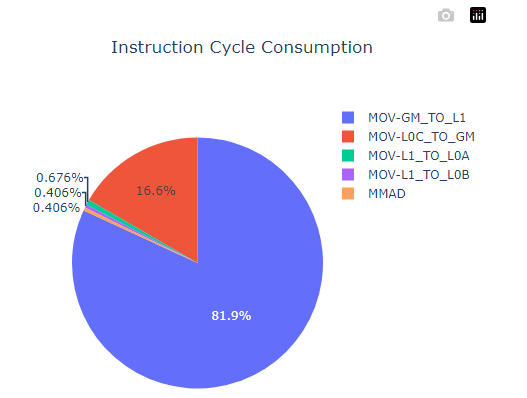
生成了指令占比饼图instruction_cycle_consumption.html,从中可以发现MOV-GM_TO_L1是算子里的最大瓶颈。
图3 指令耗时统计
父主题: 算子设计(msKPP)