文档HOT
下载
中文
注册
我要评分
文档获取效率
文档正确性
内容完整性
文档易理解
提交
在线提单
论坛求助
昇腾小AI

MmadWithSparse

功能说明

完成矩阵乘加操作，传入的左矩阵A为稀疏矩阵， 右矩阵B为稠密矩阵 。对于矩阵A，在MmadWithSparse计算时完成稠密化；对于矩阵B，在计算执行前的输入数据准备时自行完成稠密化（按照下文中介绍的稠密算法进行稠密化），所以输入本接口的B矩阵为稠密矩阵。B稠密矩阵需要通过调用LoadDataWithSparse载入，同时加载索引矩阵，索引矩阵在矩阵B稠密化的过程中生成，再用于A矩阵的稠密化。

函数原型

1
2
template <typename T = int32_t, typename U = int8_t, typename std::enable_if<IsSameType<PrimT<T>, int32_t>::value, bool>::type = true, typename std::enable_if<IsSameType<PrimT<U>, int8_t>::value, bool>::type = true>
__aicore__ inline void MmadWithSparse(const LocalTensor<T>& dstLocal, const LocalTensor<U>& fmLocal, const LocalTensor<U>& filterLocal, const MmadParams& mmadParams)

参数说明

表1 模板参数说明

参数名

描述

T

dstLocal的数据类型。

U

fmLocal、filterLocal的数据类型。

  • 当dstLocal、fmLocal、filterLocal为基础数据类型时， T必须为int32_t类型，U必须为int8_t类型，否则编译失败。
  • 当dstLocal、fmLocal、filterLocal为TensorTrait类型时，T的LiteType必须为int32_t类型，U的LiteType必须为int8_t类型，否则编译失败。

最后两个模板参数仅用于上述数据类型检查，用户无需关注。
表2 参数说明

参数名称

输入/输出

含义

dstLocal

输出

目的操作数，结果矩阵，类型为LocalTensor，支持的TPosition为CO1。

LocalTensor的起始地址需要256个元素（1024字节）对齐。

fmLocal

输入

源操作数，左矩阵A，类型为LocalTensor，支持的TPosition为A2。

LocalTensor的起始地址需要512字节对齐。

filterLocal

输入

源操作数，右矩阵B，类型为LocalTensor，支持的TPosition为B2。

LocalTensor的起始地址需要512字节对齐。

mmadParams

输入

矩阵乘相关参数，类型为MmadParams，结构体具体定义为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
struct MmadParams
{
    uint16_t m;
    uint16_t n;
    uint16_t k;
    bool isBias;
    int32_t fmOffset;
    bool enSsparse;
    bool enWinogradA;
    bool enWinogradB;
    uint8_t unitFlag;
    bool cmatrixInitVal;
    bool cmatrixSource;
};

参数说明请参考表2。

注意事项

  • 原始稀疏矩阵B每4个元素中应保证最多2个非零元素，如果存在3个或更多非零元素，则仅使用前2个非零元素。
  • M/K/N = 0表示不执行，该指令将被视为NOP并报警告。

稠密算法说明

假设原始稀疏矩阵B的每4个元素中至少有2个零，稠密化后的矩阵B是一个在每4个元素中过滤掉2个零的稠密矩阵。矩阵B稠密化的过程中生成索引矩阵，过程如下：对于稀疏矩阵B中的每4个元素，将在index矩阵中生成2个2位索引，并按照以下规则进行编码。索引必须在{0, 1, 2}范围内。

  • 第一个索引用于指示前3个元素中第1个非零元素的相对位置。
  • 第二个索引用于指示第2个非零元素在后3个元素中的相对位置。

具体可参考下表。其中，“-”表示算法不关心该位置上的值，因为其会被过滤。

示例

ele0

ele1

ele2

ele3

Index_a[i]

Index_b[i]

Two non-zero elements

0

0

X

Y

2’b10

2’b10

0

X

0

Y

2’b01

2’b10

X

0

0

Y

2’b00

2’b10

0

X

Y

-

2’b01

2’b01

X

0

Y

-

2’b00

2’b01

X

Y

-

-

2’b00

2’b00

One non-zero element

0

0

0

X

2’b00

2’b10

0

0

X

0

2’b10

2’b00

0

X

0

0

2’b01

2’b00

X

0

0

0

2’b00

2’b00

All zero

0

0

0

0

2’b00

2’b00

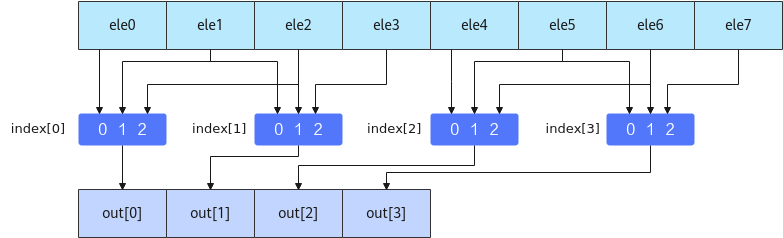
该索引矩阵用于A矩阵的稠密化，根据索引矩阵从MatrixA中的4个元素中选择2个元素参与计算，如下图所示：

支持的型号

Atlas A2训练系列产品/Atlas 800I A2推理产品

调用示例

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
#include "kernel_operator.h"

class KernelMatmul {
public:
    __aicore__ inline KernelMatmul() {}
    __aicore__ inline void Init(__gm__ uint8_t* a, __gm__ uint8_t* b, __gm__ uint8_t* idx, __gm__ uint8_t* c, uint16_t m, uint16_t k, uint16_t n)
    {
        this->m = m;
        this->k = k;
        this->n = n;

        aSize = m * k;
        bSize = k / 2 * n;
        cSize = m * n;
        mBlocks = m / 16;
        nBlocks = n / 16;
        kBlocks = k / 32;

        aGM.SetGlobalBuffer((__gm__ int8_t*)a);
        bGM.SetGlobalBuffer((__gm__ int8_t*)b);
        idxGM.SetGlobalBuffer((__gm__ uint8_t*)idx);
        cGM.SetGlobalBuffer((__gm__ int32_t*)c);
        pipe.InitBuffer(inQueueA1, 1, aSize * sizeof(int8_t));
        pipe.InitBuffer(inQueueA2, 1, aSize * sizeof(int8_t));
        pipe.InitBuffer(inQueueB1, 1, bSize * sizeof(int8_t));
        pipe.InitBuffer(inQueueIdxB1, 1, (bSize / 4) * sizeof(int8_t));
        pipe.InitBuffer(inQueueB2, 1, bSize * sizeof(int8_t));
        pipe.InitBuffer(outQueueCO1, 1, cSize * sizeof(int32_t));
    }
    __aicore__ inline void Process()
    {
        CopyIn();
        SplitA();

        AscendC::LocalTensor<int8_t> b1Local = inQueueB1.DeQue<int8_t>();
        AscendC::LocalTensor<uint8_t> idexb1Local = inQueueIdxB1.DeQue<uint8_t>();
        AscendC::LocalTensor<int8_t> a2Local = inQueueA2.DeQue<int8_t>();
        SplitB(b1Local, idexb1Local);
        Compute(a2Local);
        inQueueB1.FreeTensor(b1Local);
        inQueueIdxB1.FreeTensor(idexb1Local);
        inQueueA2.FreeTensor(a2Local);

        CopyOut();
    }

private:
    __aicore__ inline void CopyIn()
    {
        AscendC::LocalTensor<int8_t> a1Local = inQueueA1.AllocTensor<int8_t>();
        AscendC::LocalTensor<int8_t> b1Local = inQueueB1.AllocTensor<int8_t>();
        AscendC::LocalTensor<uint8_t> idxb1Local = inQueueIdxB1.AllocTensor<uint8_t>();
        AscendC::DataCopy(a1Local, aGM, { 1, static_cast<uint16_t>(aSize * sizeof(int8_t) / 32), 0, 0 });
        AscendC::DataCopy(b1Local, bGM, { 1, static_cast<uint16_t>(bSize * sizeof(int8_t) / 32), 0, 0 });
        AscendC::DataCopy(idxb1Local, idxGM, { 1, static_cast<uint16_t>(bSize / 4 * sizeof(int8_t) / 32), 0, 0 });

        inQueueA1.EnQue(a1Local);
        inQueueB1.EnQue(b1Local);
        inQueueIdxB1.EnQue(idxb1Local);
    }
    __aicore__ inline void SplitA()
    {
        int srcOffset = 0;
        int dstOffset = 0;
        AscendC::LocalTensor<int8_t> a1Local = inQueueA1.DeQue<int8_t>();
        AscendC::LocalTensor<int8_t> a2Local = inQueueA2.AllocTensor<int8_t>();

        AscendC::LoadData2dParams loadDataParams;
        loadDataParams.repeatTimes = kBlocks * mBlocks;
        loadDataParams.srcStride = 1;
        loadDataParams.ifTranspose = false;

        AscendC::LoadData(a2Local, a1Local, loadDataParams);

        inQueueA2.EnQue<int8_t>(a2Local);
        inQueueA1.FreeTensor(a1Local);
    }
    __aicore__ inline void SplitB(AscendC::LocalTensor<int8_t>& b1Local, AscendC::LocalTensor<uint8_t>& idxb1Local)
    {
        AscendC::LocalTensor<int8_t> b2Local = inQueueB2.AllocTensor<int8_t>();

        // transform nz to zn
        AscendC::LoadData2dParams loadDataParams;
        loadDataParams.repeatTimes = kBlocks * nBlocks / 2;
        loadDataParams.srcStride = 0;
        loadDataParams.ifTranspose = false;

        AscendC::LoadDataWithSparse(b2Local, b1Local, idxb1Local, loadDataParams);

        inQueueB2.EnQue<int8_t>(b2Local);
    }
    __aicore__ inline void Compute(const AscendC::LocalTensor<int8_t>& a2Local)
    {
        AscendC::LocalTensor<int8_t> b2Local = inQueueB2.DeQue<int8_t>();
        AscendC::LocalTensor<int32_t> c1Local = outQueueCO1.AllocTensor<int32_t>();

        AscendC::MmadWithSparse(c1Local, a2Local, b2Local, { m, n, k, false, 0, false, false, false });

        outQueueCO1.EnQue<int32_t>(c1Local);
        inQueueB2.FreeTensor(b2Local);
    }
    __aicore__ inline void CopyOut()
    {
        AscendC::LocalTensor<int32_t> c1Local = outQueueCO1.DeQue<int32_t>();

        AscendC::FixpipeParamsV220 fixpipeParams;
        fixpipeParams.nSize = n;
        fixpipeParams.mSize = m;
        fixpipeParams.srcStride = m;
        fixpipeParams.dstStride = n;

        fixpipeParams.ndNum = 1;
        fixpipeParams.srcNdStride = 0;
        fixpipeParams.dstNdStride = 0;

        AscendC::Fixpipe(cGM, c1Local, fixpipeParams);

        outQueueCO1.FreeTensor(c1Local);
    }

private:
    AscendC::TPipe pipe;

    AscendC::TQue<AscendC::QuePosition::A1, 1> inQueueA1;
    AscendC::TQue<AscendC::QuePosition::A2, 1> inQueueA2;
    AscendC::TQue<AscendC::QuePosition::B1, 1> inQueueB1;
    AscendC::TQue<AscendC::QuePosition::B1, 1> inQueueIdxB1;
    AscendC::TQue<AscendC::QuePosition::B2, 1> inQueueB2;
    // dst queue
    AscendC::TQue<AscendC::QuePosition::CO1, 1> outQueueCO1;

    AscendC::GlobalTensor<int8_t> aGM, bGM;
    AscendC::GlobalTensor<uint8_t> idxGM;
    AscendC::GlobalTensor<int32_t> cGM;

    uint16_t m;
    uint16_t n;
    uint16_t k;

    uint16_t aSize, bSize, cSize, mBlocks, nBlocks, kBlocks;
};

#define KERNEL_MMAD_WITH_SPARSE_OPERATOR_TEST(m, k, n)                                                             \
    extern "C" __global__ __aicore__ void kernel_mmad_with_sparse_operator##_##m##_##k##_##n(GM_ADDR a, GM_ADDR b, \
        GM_ADDR idx, GM_ADDR c)                                                                                    \
    {                                                                                                              \
        if ASCEND_IS_AIV {                                                                                         \
            return;                                                                                                \
        }                                                                                                          \
        KernelMatmul op;                                                                                           \
        op.Init(a, b, idx, c, m, k, n);                                                                            \
        op.Process();                                                                                              \
    }

KERNEL_MMAD_WITH_SPARSE_OPERATOR_TEST(16, 64, 16)
父主题： 矩阵计算
搜索结果
找到“0”个结果

当前产品无相关内容

未找到相关内容，请尝试其他搜索词